ИДЕИ
В.В.НАЛИМОВА И МАТЕМАТИЧЕСКОЕ ОБРАЗОВАНИЕ БИОЛОГОВ.
В.Н. Тутубалин,
Ю.М. Барабашева, Г.Н. Девяткова, Е.Г. Угер
Московский государственный университет им. М.В.Ломоносова.
е-mail: jbarabash@mail.ru
1. Введение.
1.1. Чем мы недовольны?
Рассуждать о каком-либо предмете имеет смысл лишь в
том случае, если мы чем-то в нем недовольны и хотим изменения к лучшему. Чем же
мы недовольны в математическом образовании биологов?
Ну, прежде всего, мы недовольны студентами. Большинство студентов какие-то вялые, ленивые, тупые, ничего не хотят делать, не знают того, что им следовало бы знать из предыдущего обучения, а если им хоть как-то удастся объяснить что-то новое, то на следующий день они все равно все забудут. Дело в том, что в МГУ издавна сложилось элитарное образование: когда мы занимаемся с группой в 25 человек каким-нибудь предметом (не важно – математическим или нет), то темп обучения рассчитывается на 5-6 лучших студентов группы, а остальные за таким темпом не успевают. В каком-то смысле это правильно, потому что в будущем эти 20% лучших будут определять уровень науки и/или образования, а пока они учатся, надо, чтобы они учились в полную силу своих способностей. И значит, 80% студентов мы фактически обрекаем на неуспеваемость.
То есть в
условиях элитарного образования лишь меньшинство студентов может чувствовать
себя комфортно в процессе обучения. На
биологическом факультете ситуация еще осложняется тем, что высшей математике (и
в частности дифференцированию и интегрированию) студентов обучают
преподаватели, которые уже ведут математические курсы на физико-математических
(или инженерных) специальностях. А им, к сожалению, до биологических применений
математики дела нет. Таким образом, определенный упрек в профессиональной
узости преподаванию высшей математики может быть предъявлен. В результате этой
узости слишком большой упор делается на искусство преобразования математических
формул (копируется сложившаяся в физико-математическом цикле традиция). А это
искусство будущим биологам, во-первых, не очень нужно (поскольку не дает в
биологии такого успеха, к которому мы привыкли в физике), а во-вторых, не всеми
может быть усвоено.
Преподаватели математики на любом факультете МГУ – это,
конечно, элита из элит, и их нельзя упрекнуть (как студентов) в тупости или
лености. Однако содержание образования (от которого в первую очередь зависит,
сколько процентов студентов могут это образование понять) формируют в конечном
счете не те преподаватели, которые лично читают лекции или ведут занятия, а
выдающиеся ученые, научные результаты которых и определяют на десятилетия (если
не на века) вперед, что именно будут изучать студенты.
У А.Н. Колмогорова есть работа под названием «Реальный
смысл результатов дисперсионного анализа» [1].
Эта работа написана в конце 40-ых годов (опубликована в 1950-ом). В ней
Колмогоров критикует Р.А.Фишера в отношении интерпретации результатов
дисперсионного анализа. Однако он неоднократно повторяет, что, несмотря на отмечаемые
недостатки, метод дисперсионного анализа Фишера весьма полезен. А вот это
высказывание Колмогорова голословно: никаких примеров пользы дисперсионного
анализа он не приводит. Но Колмогоров обладал и обладает высочайшим научным
авторитетом, и в результате метод дисперсионного анализа, в частности, попал в
учебник по математике для биологов второго курса [2].
Другой пример относится к описанию динамики
численностей биологических популяций. В 20-е годы прошлого века в работах Лотки
и Вольтерра появились математические модели в виде систем дифференциальных
уравнений, якобы описывающих эту динамику, а среди них - знаменитая модель
«хищник-жертва», состоящая из двух уравнений. Она написана таким образом, что
допускает явное решение, и в результате оказывается, что на фазовой плоскости
имеется особая точка типа центра, вокруг которого происходят периодические во
времени движения по некоторым траекториям. Колмогоров, поправляя Вольтера,
публикует собственную работу на эту тему. Суть ее сводится к тому, что предложенная
Вольтерра модель не является достаточно «грубой»: небольшое изменение правых частей уравнений приводит к тому, что
особая точка типа центра может превратиться в точку другого типа (узел, фокус,
седло, и т.д.). В частности, вполне возможно появление предельного цикла вместо
движения по периодическим траекториям. Конечно, Колмогоров совершенно прав: уж
если рассматривать дифференциальные уравнения применительно к динамике
популяций, то могут иметь биологический смысл лишь грубые модели. Вот и попадает
в учебник для биологов второго курса идея вместо рассмотрения биологически
значимых моделей изучение
качественного поведения решений систем дифференциальных уравнений. Но априори такая идея вообще абсурдна. Для
того, чтобы асимптотическое поведение (за большое время) решений
дифференциальных уравнений имело биологический (или иной прикладной) смысл,
нужно, чтобы поведение реальной системы за малое время весьма точно описывалось
теми производными, значения которых стоят в правых частях уравнений. Этого не
может быть в биологии хотя бы потому, что уравнения Лотки и Вольтерра не
учитывают многих биологических факторов, реально влияющих на динамику
популяций. Помещение в учебник для студентов идеи качественного исследования
дифференциальных уравнений может быть оправдано лишь апостериори: путем приведения хотя бы одного примера, в котором
теория и действительность оказались сколько-нибудь похожими. Но ничего
подобного в этом учебнике нет. Единственное, на что может рассчитывать модель
дифференциальных уравнений в смысле описания динамики популяций – это описание
изменений за сравнительно короткое время, например, с целью прогноза. Но это
должно быть более или менее количественное описание, и оно должно
подтверждаться реальными примерами.
1.2. Мысли В.В. Налимова
После ликвидации Межфакультетской лаборатории
статистических методов («лаборатория Колмогорова») Биологический факультет МГУ
гостеприимно приютил В.В. Налимова и группу его сотрудников. Понятно, что после
этого возник вопрос о применении математики в биологии с научной и образовательной точек зрения.
Что касается научной стороны, то в устных беседах и выступлениях Василий
Васильевич неоднократно говорил о том, что математика в биологии используется
далеко не в полную силу ее возможностей, и выдвигал идею «геометризации
биологии». При этом имелось в виду нечто, напоминающее его «вероятностную модель языка»: изначально
имеется некий континуум биологических смыслов (который для наглядности можно
представлять себе в виде числовой оси). В процессе же биологической эволюции
происходит его «распаковка» с помощью некоторых фильтров, в результате чего
возникают отдельные особи, биологические виды, популяции, таксономические
единицы и т.д.
Каким образом столь общий подход может быть
сколько-нибудь содержательным? Для ответа на этот вопрос следует остановиться
на одном положении научной философии В.В. Налимова, согласно которому научное
знание представляет собой совокупность некоторых метафор. В ХХ веке большую популярность и влияние имело философское
направление, получившее название «философии науки». Ряд представителей этого
направления, рассматривая структуру научной теории в своих работах, убедительно
показали, что любой эксперимент является «теоретически нагруженным» [3], т.е. в самой постановке
эксперимента, в используемых терминах неявным образом содержатся теоретические
предпосылки. Тем самым можно сказать, что ни эксперимент, ни научная теория не
являются абсолютно надежными, поскольку они взаимно обусловлены.
Остроумие и убедительность этих работ позволяют с
уверенностью утверждать, что традиционно-позитивистское понимание науки никуда
не годится. Однако, несмотря на отсутствие «твердого» экспериментального
фундамента, науке все же удается находить новое знание. Философия науки как
высшее достижение современного рационального мышления, по всей видимости,
объяснить феномен нового знания не в
состоянии. Может быть единственное, что остается в таких условиях это признать,
что научное знание достигается принципиально так же, как и религиозное, т.е. в
результате чуда и откровения – понятий, находящихся вне философии науки. А наши
научные теории и эксперименты не более чем научные метафоры, которые иногда
даже имеют некоторое сходство с истиной.
В таком случае почему бы и не допустить, что
«распаковка» биологического континуума могла бы сделать (на уровне метафоры)
некоторые вещи в биологии более понятными. Однако Василий Васильевич, к
сожалению, не оставил подробной разработки этой идеи.
Он думал, конечно, и о математическом образовании
биологов на том научном уровне, который уже есть, надеясь, быть может, на то,
что если молодые люди получат хорошее математическое и биологическое
образование, то кто-нибудь из них осуществит в будущем и «геометризацию
биологии». Он даже делал конкретные предложения о создании новой специальности.
Однако эти предложения пришлись на такой отрезок времени, когда руководящие
образованием органы не могли и не хотели думать о каких-то новшествах.
В настоящее время обновление образования в России
реально происходит. Например, в МГУ открыто много новых факультетов.
Сравнительно беспрепятственно издаются в бумажном виде многие новые учебники, а
главное – стал широко доступен Интернет, который начисто снимает проблему
публикации чего угодно. Можно подумать и об обновлении математического
образования биологов – если не в рамках создания новой биолого-математической
специальности (для чего нет реальных не столько образовательных, сколько
научных возможностей: см. об этом ниже), то хотя бы в рамках совершенствования
существующего образования. Конечно, при этом могут быть использованы лишь
некоторые частные идеи В.В. Налимова.
Эта работа представляет собой сообщение о попытках
разработки таких идей. Взявшись за эту задачу, авторы с удивлением убедились,
что находящийся в обращении научный материал далеко не достаточен для
реализации в преподавании даже самого простого из того, что предлагал Василий
Васильевич. Курс «Математические методы в биологии», который преподается на
биофаке сотрудниками бывшей лаборатории Налимова, состоит из двух частей: 1.
теория вероятностей и математическая статистика; 2. математические модели в
биологии (главным образом, модели динамики численности популяций). В
соответствии с этим речь в данной статье идет о двух научных разработках с
ориентацией на использование в преподавании: 1. анализ некоторых генетических
экспериментов с помощью математико-статистического метода эмпирических функций
распределения (использующего известный критерий Колмогорова); 2. математические
модели для анализа экспериментов Гаузе по конкуренции видов.
2.
Вероятностно-статистические методы в образовании биологов
2.1. Выбор «носителя информации» для целей обучения.
Цель математического образования - овладеть
математическими методами. А вот наши
методы обучения сходны с методами исихастов[1].
В самом деле, на первом курсе студенты должны вычислить много производных и
интегралов от функций, которые сами по себе никакого интереса не представляют,
но только таким образом достигается умение обращаться с математическими
формулами. Это умение не столь возвышенно, как соединение с Богом у исихастов,
но для понимания и, возможно (хотя бы для части студентов), для дальнейшего
развития наук физико-математического цикла крайне важно. Ведь откровение в этих
науках нередко приходит через математические формулы.[2]
В.В. Налимов неоднократно подчеркивал, что физические
формулы (например, уравнение Шрёдингера) отличаются тем, что необычайно богаты
следствиями. Владение формулой означает способность видеть, какие следствия из
нее вытекают. А как развить эту способность, иначе как путем вычисления
интегралов и производных по примеру исихастов?
Кроме формул, в математике есть, конечно, еще и
понятия, и теоремы. Математические курсы строятся как длинные логические
цепочки исходных понятий и их следствий. При этом не существует каких-либо
эффективных представлений о том, как именно следует выстроить ту или иную
длинную логическую цепочку, чтобы получить доказательство нужной теоремы.
Далеко не все студенты одарены такими способностями, которые позволяют им
видеть нужные пути преобразования математических формул, либо построения
математических доказательств. Более того, встречаются математические учебники,
анализ которых показывает, что их авторы хоть и преподают математику, но сами
не умеют выстроить математические доказательства достаточно коротким и
эффективным путем. Таким образом, когда авторы учебников для студентов
нематематических специальностей выписывают, например, формулу для плотности
двумерного нормального закона, они напрасно тратят бумагу. Эллипсов рассеивания
снарядов за этой формулой студенты не увидят.
Но есть и другая, еще более фундаментальная причина,
по которой копирование в облегченном виде физико-математического образования
неприемлемо для студентов-биологов. Если в физике откровение избирает для
своего проявления математические формулы (не любые, конечно, формулы, но хотя
бы некоторые – те, которые по таинственным причинам оказались наиболее
удачными), то в биологии этого не происходит.[3]
В общем, математические формулы и математические
доказательства – это неподходящий «носитель информации» для обучения будущих
биологов. На всё, конечно, нужно иметь вкус и меру: простые формулы и простые
доказательства следует сохранить. Но вот наступает, например, момент, когда
изучается регрессия: сначала парная, а затем и множественная. Что же, записать
необходимые формулы в терминах обращения матриц? Но что с этими обратными
матрицами будут делать студенты, кроме заучивания их наизусть? К счастью, в
нашу компьютерную эпоху имеется избавление в виде пакетов программ (Excel, Statistiсa, и пр.). Для
пользования такими пакетами вообще не обязательно знать, какие формулы лежат в основе
вычислений. И это, конечно, вполне в духе идей В.В. Налимова. Дело в том, что
формулы, подобные упомянутым формулам регрессионного анализа, употребляются в
математической статистике для оценки той точности, с которой можно определить
по экспериментальным данным параметры модели, в частном случае – коэффициенты
регрессии. Отказываясь от формул, мы лишаемся оценки этой точности. Но оценки
точности основываются на некой не имеющей обоснования вероятностной модели,
которой должны следовать исходные данные, а эта модель, согласно В.В. Налимову,
может быть лишь метафорой. Что касается самих
параметров, то эта метафора может быть приемлемой, но в оценке точности
их определения обычно бывает прескверной, и этим оценкам все равно нельзя
доверять. В конце концов, не так уж важно, с чего начинать метафору: с
математической формулы или с нескольких щелчков компьютерной мышкой.
Таким образом, возникает идея заменить (в значительной
мере) изучение математической части теории вероятностей и математической
статистики на работу с компьютерными пакетами программ.
Предварительно напомним, что поле приложения
вероятностно-статистических методов для общебиологических специальностей одно:
обработка результатов наблюдения с целью ослабления влияния случайных ошибок
(включая планирование эксперимента). Ориентация на обработку наблюдений давно
(и правильно) сложилась, и речь может идти лишь о введении частных улучшений.
Следует также помнить мысль, которую В.В. Налимов высказывал неоднократно: курс
теории вероятностей и математической статистики лучше начинать с математической
статистики. В самом деле, если курс начинается с бросания монеты или извлечения
шаров из урны, то студенты не понимают, зачем этот курс нужен биологу. Хорошо
бы начать прямо с какого-то биологического приложения.
Но очевидно, что при изложении приемов математической
статистики в их биологическом приложении мы привязаны к доступной
экспериментальной информации. Необходимым требованием к этой информации (помимо
доступности) является и ее достаточно понятная биологическая интерпретация.
2.2. Предлагаемый пример
Каким должен быть пример для демонстрации возможностей
вероятностно-статистических методов в биологии? Имеется ряд измерений
биологических характеристик, записанные в том порядке, в котором они были получены.
Возможно, что в этом ряду имеются какие-то детерминированные тенденции,
связанные с переменой условий наблюдения в пространстве и/или времени. Конечно,
прежде всего нужно выявить эти тенденции. Хорошо, если заранее известны
переменные значения каких-то факторов, которые могут повлиять на наблюдения.
Тогда можно изучать связь этих факторов с наблюдениями, обращаясь к
вероятностным методам. Если заранее такие факторы не известны, то надо хотя бы
проверить, что значения измеряемой величины не зависят систематически от номера
наблюдения. Для этой цели нужно попросту нарисовать график, по оси абсцисс
которого откладывается номер наблюдения, а по оси ординат – значение измеряемой
величины. В таком графике нет ничего от теории вероятностей. Несколько более
утонченный прием – это график кумулятивной суммы наблюдений (как функции от
числа слагаемых). Должна получиться примерно прямая линия. Эти два приема
первичной обработки данных должны применяться всегда.
Если никаких систематических тенденций в наблюдениях
выявить не удается, то можно предположить (в качестве гипотезы), что порядок
наблюдений вовсе не важен. В этом случае вся содержащаяся в наблюдениях
информация отражается (без существенных потерь) в эмпирической функции
распределения. Опять-таки, можно предполагать или не предполагать вероятностную
природу наблюдений, т.е. допускать или не допускать, что за этой эмпирической
функцией распределения стоит некая истинная,
или теоретическая функция распределения случайной величины.
К сожалению, в
наиболее популярных компьютерных пакетах (таких, как Excel или Statistica)
рисование эмпирической функции распределения непосредственно в меню пакета не
предусматривается, хотя легко может быть осуществлено средствами пакета.
Студентов, конечно, нужно этому научить. Если принять вероятностную точку
зрения, то приемы, основанные на эмпирической функции распределения, являются
самыми предпочтительными, поскольку промежуточным этапом в этом случае является
глазомерный анализ всей экспериментальной информации, практически без потерь.
Гистограмма, влекущая группировку данных, в этом смысле хуже, т.к. неизбежно
огрубляет информацию.
Одним из известным нам примеров демонстрации
возможностей эмпирической функции распределения (примером, для которого есть
фактические данные, а также понятен биологический смысл тех выводов, которые
можно сделать из статистической обработки) является частота появления тех или
иных фенотипов или генотипов, которые возникают при скрещивании различных
сортов гороха. Г.Мендель выделил для гороха 7 «менделирующих» признаков [4]. Остановимся на признаке «окраска
семядолей»: желтая окраска – доминантный признак, зеленая – рецессивный.
Первоначально имелось в виду приспособить для
преподавания тот фактический материал, который использован в известной работе
Колмогорова [5]. Однако оказалось,
что для этой скромной цели дополнительно нужна научная разработка некоторых
вопросов. Эта разработка подробно описана в работе [6], а здесь мы лишь кратко изложим результаты.
Желтые и зеленые горошины в опыте пересчитываются по
отдельным плодам (бобам), и в идеале
именно эти данные следовало бы иметь для статистической обработки. Но доступными оказались только обобщенные
данные, а именно: число желтых и зеленых горошин по отдельным «семьям»
поколения F2 («семьей» называются все горошины, полученные от одного
растения). Колмогоров предложил рассматривать нормированное число
«успехов» (под «успехом» понимается появление желтой горошины, вероятность
успеха р теоретически равна
¾), а именно, для каждой семьи с номером к ввести величину
, (1)
где 
k – число успехов, nk – численность семьи. При достаточно больших
численностях отдельных семей nk числа {xk} должны образовывать выборку из стандартного
нормального закона N(0,1). Последнее утверждение предлагалось проверять с
помощью критерия Колмогорова.
Сам Колмогоров образовал две такие выборки по данным
Ермолаевой [7]. При повторении
вычислений Колмогорова у нас не получилось точного совпадения с его графиками,
приведенными в [5]. Однако различия
не имеют существенного значения, а наши
результирующие чертежи показаны на рис.1а и 1б. Глазомерно совпадение
хорошее, вычисление статистики Колмогорова также дает незначимое отличие от N(0,1), так
что вслед за Колмогоровым мы можем сделать вывод, что опыты Ермолаевой, которые
подавались автором как опровержение законов Менделя, на самом деле являются
подтверждением этих законов.
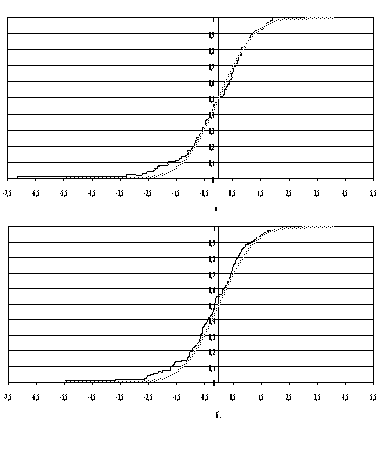
Рис.1. Эмпирические функции распределения
нормализованных
данных
Ермолаевой [7]: а - таблица 4; б - таблица 6.
Какая же тут нужна научная разработка?
Неясные вопросы начинаются, если перерисовать рисунки
1а и 1б в нормальном масштабе (рис.2а и 2б). Рисунки в нормальном масштабе дают
типичную картину «тяжелого левого хвоста» для эмпирической функции распределения.
Глядя на эти картинки, невозможно согласиться с тем, что соответствующее
теоретическое распределение является нормальным. Колмогоров, очевидно, не
рисовал этих картинок, поскольку говорит о данных Ермолаевой как о «новом,
блестящем» подтверждении законов Менделя. Подтверждение есть (основная часть
экспериментальных данных удовлетворяет стандартному нормальному закону, и лишь
небольшая часть данных в левом хвосте с ним не согласуется), но не блестящее, а
довольно скромное.
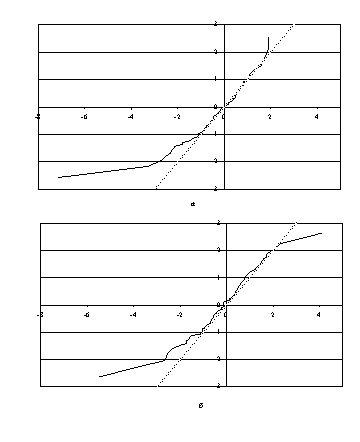
Рис.2. Эмпирические функции распределения данных Ермолаевой
в нормальном
масштабе: а - таблица 4; б - таблица 6.
Но может быть, «тяжелые хвосты» имеют чисто
математическое объяснение? Дело в том, что численности отдельных семей в данных
Ермолаевой часто невелики (порядка одного
десятка и даже единиц). Может быть, применение предельной теоремы
Муавра-Лапласа в данном случае слишком грубо? В наше время с помощью компьютера
нетрудно рассчитать тот «теоретический идеал», на который должна быть похожа
эмпирическая функция распределения величин {xk} (т.е. математическое ожидание значений этой
эмпирической функции в точках х с
достаточно малым шагом по х). Расчет показывает, что «тяжелый
левый хвост» у этого «идеала» действительно появляется, но при столь малых
вероятностях, которые не могут быть связаны с данными Ермолаевой.
Рассчитать точное распределение статистики Колмогорова
для тех численностей семей, которые наблюдались в опытах Ермолаевой, мы не
сумели. Но расчеты с помощью метода Монте-Карло показали (рис.3), что точная
функция распределения заведомо лежит правее функции распределения Колмогорова.
Это означает, что те значения статистики Колмогорова, которые признаются
незначимыми с помощью распределения Колмогорова, окажутся тем более
незначимыми, если воспользоваться точной функцией распределения.
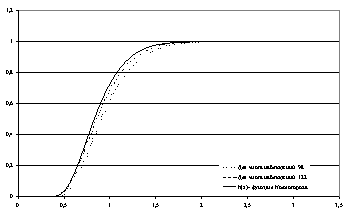
Рис.3. Сравнение функций распределения статистик l с фукцией Колмогорова K(x)
Таким образом, «тяжелые хвосты» в данных Ермолаевой не
имеют математического объяснения. Следует ли расценить их как реальное указание
на не вполне точное выполнение закона расщепления признаков или как ошибку
эксперимента? С целью ответа на этот вопрос мы рассмотрели экспериментальные
данные сторонника менделевской теории Енина [8] и обнаружили, что для этих данных закон расщепления признаков
выполняется более точно, чем теоретически возможно. Впрочем, среднее значение
нормированных чисел успеха оказывается значимо отличным от нуля, а стандартное
отклонение равно 2/3 вместо 1 (рис.4). Видимо, речь может идти о том, что в
публикации приведены не все экспериментальные данные. Тот факт, что с помощью
статистического анализа может быть вскрыта возможная фальсификация результатов
эксперимента, тоже, несомненно, должен быть представлен в преподавании для
студентов.
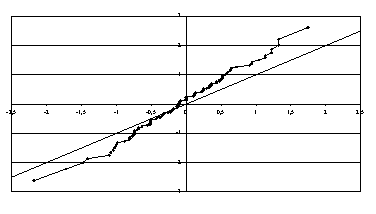
Рис.4. Эмпирическая функция распределения
для данных Енина [8]
в нормальном масштабе.
Но Енин в
настоящее время – малоизвестная фигура. Гораздо интереснее рассмотреть с этой
точки зрения данные самого Г. Менделя. В своей классической работе Мендель
приводит очень большое количество данных. Часть из них можно назвать
«биномиальными»: они касаются расщепления по одному признаку и укладываются в
схему (1), описанную выше. Часть же данных касается расщепления по двум и трем
признакам, и эти данные укладываются в схему полиномиальных испытаний, т.е. испытаний,
каждое из которых имеет несколько исходов, причем вероятности каждого
отдельного исхода Мендель указывает из теоретических соображений. Для
сопоставления реально наблюдаемых частот с теоретическими вероятностями обычно
применяется критерий хи-квадрат К.Пирсона. Таким образом, обработка всех
наблюдаемых частот отдельных исходов сводится к вычислению одного числа. Уже с
начала ХХ века известно, что если эту методику применить к результатам Менделя,
то будут получаться слишком малые значения статистики хи-квадрат. Сложение всех этих чисел (и степеней свободы)
дает такой результат, который не оставляет сомнений в том, что данные Менделя
были каким-то образом фальсифицированы, т.к. получается несомненно слишком
малое значение результирующей статистики.
По нашему мнению, приемы А.Н. Колмогорова, связанные с
эмпирической функцией распределения, должны выдвигаться на первый план в
преподавании математической статистики (потому что анализируются сами исходные
данные, полученные в опыте, а не результаты вычисления отдельных статистик).
Поэтому критерий хи-квадрат может быть заменен исследованием на нормальный
закон некоторых независимых линейных комбинаций из частот отдельных исходов
полиномиальных испытаний (подробнее см. [6]).
Таких комбинаций будет всего на единицу меньше, чем число различных исходов
отдельного полиномиального испытания. Этот прием мы назвали
«колмогоровизацией». С помощью этого приема все данные Менделя (как
биномиальные, так и полиномиальные) можно свести к независимым наблюдениям,
имеющим стандартное нормальное распределение. Стандартное отклонение,
подсчитанное по этой выборке, составляет около 2/3 (как и для данных Енина).
Критерий Колмогорова отвергает теоретическую гипотезу на уровне 0.05, что не
столь решительно, как для критерия хи-квадрат, но все-таки и при использовании
этого критерия возникают сомнения в данных Менделя.
К этому можно прибавить результат, не опубликованный в
[6]. Последняя работа (в ее
Интернет-публикации) вызвала некоторый отклик. Мы горячо благодарны Н.Н.
Хромову-Борисову за предоставление
электронной копии статьи Дарбишира [9]
и в особенности за присылку текстового файла таблиц этой статьи. На рис.5
показаны в нормальном масштабе «колмогоровизированные» данные по объединению
всех таблиц этой статьи. Видно, что согласие c N(0,1) превосходное, включая хвосты эмпирического
распределения.
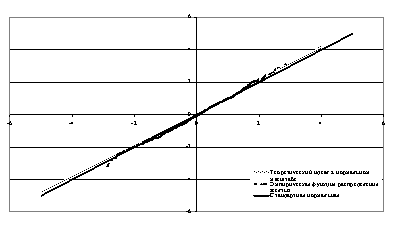
Рис.5. Данные Дарбишира [9] в нормальном масштабе.
Что еще можно извлечь из данных по расщеплению
признаков? Рассмотрим такой важный признак, как урожайность. Урожайность можно измерять
в центнерах с гектара, а можно и в «самах»: например, урожай «сам-десять»
означает, что осенью с поля собрали в десять раз больше, чем весной посеяли
семян. Если пренебречь тем, что некоторые горошины поколения F2, будучи
посеяны, могут вообще не взойти (либо не дать полноценных растений), то размер
отдельной семьи и есть урожайность «в самах» отдельной горошины. Складывая,
следовательно, вместе число желтых и зеленых горошин, получаем отдельное
наблюдение этой урожайности. Таким образом, можно обрабатывать эти числа,
предполагая, что они образуют выборку.
Но прежде всего следует проверить гипотезу об
одинаковом теоретическом распределении рассматриваемых величин. Чтобы это
сделать, нужно предложить какую-то альтернативу к проверяемой гипотезе: как именно
может нарушаться постоянство распределения вероятностей. В случае урожайности
это может происходить при переменном «плодородии» почвы, в зависимости от
местонахождения растения. Конечно, никаких данных о положении отдельных
растений таблицы состава семей по менделирующему признаку не содержат. Но можно
предположить, что нумерация семей, т.е. отдельных растений, происходит подряд.
Тогда положение растения на почве связано с его номером в таблице. Вот и будем
изучать, не меняются ли вероятностные свойства наблюдений в зависимости от
порядкового номера наблюдения. Простейший способ для этого – это образование
кумулятивной суммы. При постоянстве математического ожидания наблюдений
естественно ожидать (в силу закона больших чисел), что график кумулятивной суммы
(в зависимости от числа слагаемых) будет зрительно схож с прямой линией. Если
это математическое ожидание меняется, то график будет искривляться (вести себя
примерно как сумма математических ожиданий отдельных слагаемых). В случае
данных Ермолаевой (таблицы 4 и 6 из [7]) результат показан на рис.6а. Каждая таблица
дает примерно прямую линию, но угол наклона ее к оси абсцисс больше для
данных таблицы 6, что означает, что для
этих данных среднее значение урожайности выше.
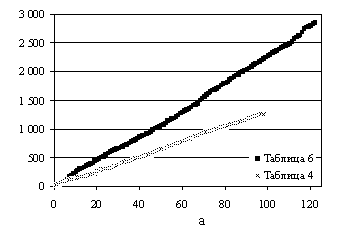
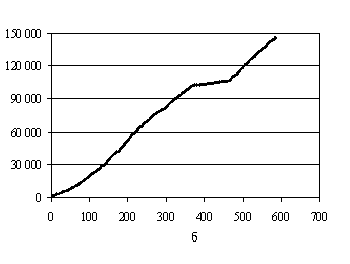
Рис.6. Графики кумулятивной урожайности:
а – данные Ермолаевой; б – данные Дарбишира (все
таблицы вместе).
Поскольку однородность данных таблицы 4 и таблицы 6
(каждой в отдельности) данным простейшим тестом не отвергается, можно
предположить, что эти данные представляют собой выборки. Для приобретения опыта
в обращении со статистическими критериями можно подтвердить вывод об
однородности данных Ермолаевой еще с помощью критерия Колмогорова-Смирнова.
Данные Енина также выдерживают тест на статистическую
однородность. А вот если объединить все таблицы Дарбишира [9], то кумулятивная кривая имеет явное отклонение от прямой линии
(рис.6б). Это частично объясняется тем,
что часть экспериментов Дарбишира относится к так называемой «контрольной
группе», растения которой были выращены на менее удобренной и хуже обработанной
почве, чем растения экспериментальных групп.
3. Модели
для динамики численностей биологических популяций.
В 20-ых годах прошлого века, когда Лотка и Вольтерра
опубликовали свои работы, возникла мечта о создании «математической теории
борьбы за существование», которая была бы способна количественно выразить те
закономерности, которые возникают в процессе этой «борьбы». Биологи понимали,
по-видимому, что в природных биологических сообществах вряд ли могут
действовать модели дифференциальных уравнений, поскольку в природе ситуация
слишком сложна. Но возникал вопрос: есть ли надежда на то, что хотя бы в
условиях тщательно стабилизированного лабораторного эксперимента можно получить
количественное согласие между биологической реальностью и решениями систем
дифференциальных уравнений? Фактически предлагалось не описать какую-то
биологическую реальность с помощью математической модели, а наоборот подогнать
биологический эксперимент под готовую модель. Такого рода эксперименты делались
многими исследовательскими группами, но если говорить о материалах, пригодных
для преподавания студентам, то «свет сошелся клином» на работах Г.Ф. Гаузе по
очень простой причине: Гаузе опубликовал достаточно подробные данные
экспериментов, включая данные по отдельным повторностям эксперимента.
Что касается модели «хищник-жертва», то, Гаузе не
говорит о каком-либо количественном согласии экспериментальных данных с этими
уравнениями, и не пытается даже определить из эксперимента значения параметров
уравнений. Ему всего лишь удается в эксперименте осуществить периодические
колебания численности «хищника» и «жертвы», качественно похожие на те, что
предсказывает теория. Это становится возможным при внесении в эксперимент
дополнительных условий, которые отнюдь не предусмотрены теорией (создание
убежищ для жертв, иммиграция и т. д.). И в этом случае модель Вольтерра
является метафорой в смысле В.В. Налимова. Здесь студенту предъявить нечего.
Более благоприятна ситуация с моделью конкуренции двух
видов за общий ресурс. Здесь параметры уравнений определяются из эксперимента и
производится сопоставление их решений с фактическими данными. Существует две
группы работ Гаузе на эту тему: в одной группе речь идет о конкуренции видов
дрожжей, а в другой – о конкуренции инфузорий. Математическая модель в обоих
случаях почти одинакова, отличаясь лишь некоторыми деталями. Выпишем уравнения
модели.
1) В случае одновидовой популяции рассматривается
уравнение логистического роста численности популяции N(t)
(2)
где
b –
коэффициент экспоненциального роста популяции, К – предельная численность популяции. Это уравнение интегрируется,
а получаемое решение удобно записать в следующих терминах. Введем величины 
Эти величины
экспоненциально убывают, т.е. эволюционируют по закону 
Таким образом,
графическая проверка логистического закона состоит в том, что в какие-то
моменты времени 
определяются
экспериментальные численности популяции 
, по ним определяется максимально возможная численность К, а затем вычисляются логарифмы величин
которые должны (как
функции от времени) примерно лечь на прямую линию. Угловой коэффициент этой
прямой дает оценку для (-b). Значения N(tk), близкие к предельной численности К (и дающие отрицательные значения y(t)) , при этом
во внимание не принимаются.
Теоретические численности вычисляются по формуле 
Упражнения на логистический рост для студентов должны
входить в курс математических методов для биологов. Такие упражнения легко осуществимы в пакете Excel. В
качестве исходных данных можно использовать данные Гаузе о росте дрожжей,
приведенные в [10].
Что касается
данных об инфузориях, то логистический закон роста (для одновидовых популяций)
в этом случае не подтверждается. Это тоже студенты могут установить сами.
2) В случае двух конкурирующих видов уравнения для
численностей имеют вид
Параметры 
в этих уравнениях
подбираются по данным о росте одновидовых популяций и лишь определение
параметров a и b (которые называются параметрами взаимовлияния видов) требует экспериментов по совместному
выращиванию.
С системой уравнений конкуренции связано ее
качественное исследование, называемое теоремой
Гаузе. Доказательство этой теоремы вполне доступно для студентов-биологов,
как только они поняли, что уравнения конкуренции задают скорость движения по
интегральным кривым. А знать это доказательство нужно вот зачем.
Существует расхожая точка зрения, что Гаузе сформулировал так называемый закон конкурентного исключения, в
соответствии с которым биологические виды, имеющие одну и ту же экологическую
нишу, не могут сосуществовать одновременно длительное время: один из них
вытесняет остальные в процессе конкурентной борьбы. На самом деле Гаузе имел в
виду всего лишь частный случай своей теоремы, относящийся к варианту 
, интерпретируя это как конкуренцию за один и тот же общий
ресурс. В этом случае, действительно, с
течением времени численность одного из видов должна стремиться к нулю.
Применимость этой теоремы к реальным биологическим системам находится под
большим вопросом, так как даже в специальных экспериментах, предназначенных для
того, чтобы получить сходство с решениями уравнений конкуренции, такое сходство
едва ли получалось. Кроме того, теорема Гаузе не имеет отношения к конкуренции
трех и более видов. Наконец, качественное исследование системы дифференциальных
уравнений имеет тот недостаток, что оставляет неизвестным, за какое именно
время достигается то или иное предельное поведение.
Возможно ли изучать со студентами применение модели конкуренции к данным
Гаузе? Данные о росте одновидовых
популяций дрожжей хотя бы грубо соответствуют логистическому закону. Что
касается совместного культивирования двух видов дрожжей, то вполне возможно так
подобрать коэффициенты взаимовлияния видов, что решения уравнений конкуренции
будут похожи на фактические данные примерно в той же мере, в какой одновидовые
данные похожи на логистические кривые (рис.7а, 7б). Однако сама возможность
приближения экспериментальных данных кривыми, зависящими от многих параметров
(для уравнений конкуренции параметров шесть), мало о чем говорит. Необходимо
проверить полученное приближение на
других аналогичных опытах, либо вложить альтернативный биологический смысл в
полученные параметры с возможностью их количественной оценки (подробнее см. [12]).
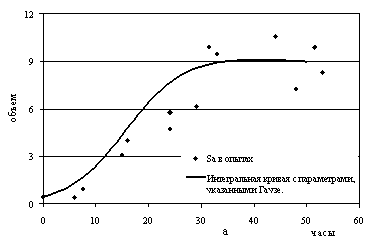
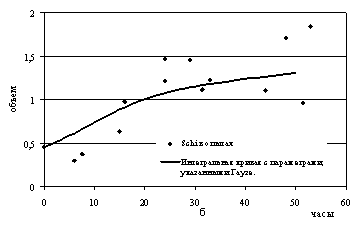
Рис.7. Рост видов дрожжей в смешанной популяции:
а - Saccharomyces cerevisiae;
б - Schizosaccharomyces
kephir.
Что касается экспериментов Гаузе с инфузориями [11], то математическая часть этих
работ, вполне достойная в статьях с дрожжами, становится не вполне корректной
(подробности см. в [10]). Таким
образом речь может идти лишь о новой математической обработке данных Гаузе.
Мы предприняли такую обработку. Вкратце, она состояла
в следующем (подробное изложение см. в [10]).
Прежде всего, наблюдения Гаузе редки во времени (за сутки, протекающие от
одного пересчета до другого, численность видов может измениться в несколько
раз). Следовательно, дифференциальные уравнения неуместны и должны быть
заменены рекуррентными. Из логистической модели вытекают такие рекуррентные
уравнения, которые не согласуются с экспериментальными данными. Поэтому
линейное убывание логарифмической скорости роста одновидовых популяций заменяем
более медленным - экспонента, стремящаяся к нулю. Результат сглаживания
логарифмических скоростей роста представлен на рис.8а и 8б. То есть для
одновидовых популяций получается неплохо. Эта мысль – о том, что данные с
большим разбросом все-таки могут сглаживаться методом наименьших квадратов –
вполне может быть донесена до студентов.
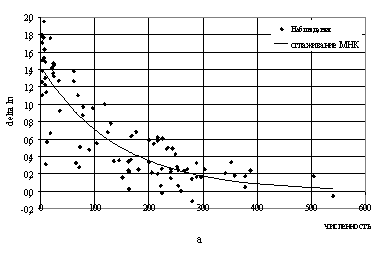
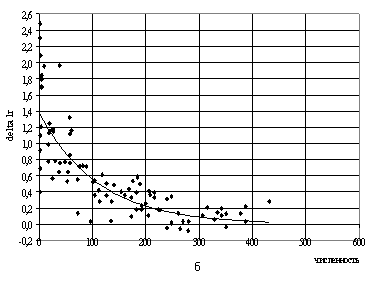
Рис.8. Логарифмические приращения численности в зависимости
от численности
вида (данные табл.4 [11], все значения m)
а) P.aurelia: DlnN=c1*exp(-c2*N);
c1=1.424; c2=0.007;
б) P.bursaria: DlnN=c1*exp(-c2*N); c1=1.3845;
c2=0.0091.
Затем
переходим к совместному культивированию видов. Исходные данные очень неточные.
Остановимся на аналоге уравнений конкуренции, когда логарифмическая скорость
роста каждого вида зависит лишь от линейной комбинации численностей обоих
видов. Подбор параметров взаимовлияния a и b производим по части данных, относящихся к опыту с
прореживанием m = 0.1. В таком случае испытанием модели является
применение тех же параметров для оставшихся данных (варьируется прореживание
популяций m и/или начальные условия). Успех лишь частичный: в
случае m = 0.2
теоретические численности похожи на реальные данные (рис.9а, 9б) а в
случае m = 0.3 нет.
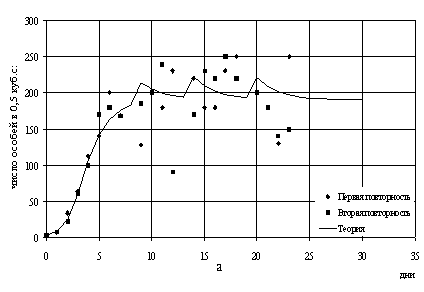
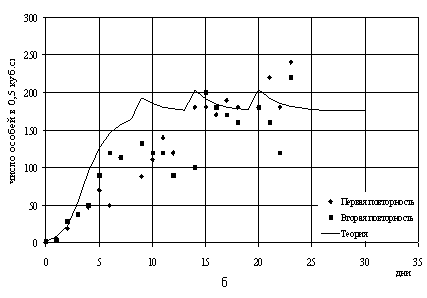
Рис.9. Теоретические и наблюдаемые численности в
смешанной популяции
с параметрами a=0.8, b=0.4 m=0.2: а - P.aurelia; б -
P.bursaria.
Заключение.
Для первой
(вероятностно-статистической) части курса математических методов в биологии
могут быть найдены фактические данные, имеющие понятный биологический смысл и
дающие возможность проиллюстрировать эффективность математических методов. Но
что касается второй части курса (математическое моделирование в биологии), то
положение печально. Мы сталкиваемся с постепенно выявившейся научной
несостоятельностью того направления, начало которому было положено в работах
Лотки и Вольтерра. И надо отдать должное Г.Ф. Гаузе, который (несмотря на все
частные недостатки своих работ) фактически делает (в конечном счете) этот самый
вывод – о несостоятельности попыток моделирования динамики популяций с помощью
примитивных схем дифференциальных уравнений. Хотя в своих более ранних работах
Гаузе всячески славит имеющую в ближайшем будущем явиться «математическую
теорию борьбы за существование».
Литература
1.
Колмогоров А.Н. Реальный смысл
результатов дисперсионного анализа.// Труды 2-го Всесоюзного совещания по
математической статистике в Ташкенте в 1948 г. Изд. АН УзССР, Ташкент, 1949,
стр. 240-268.
2.
Мятлев В.Д., Панченко Л.А., Резниченко
Г.Ю., Терехин А.Т. Теория вероятностей и математическая статистика.
Математические модели. (В серии «Высшая математика для биологов:
университетский учебник») М., Academia, 2009.
3.
Поппер К. Логика научного
исследования. Гл.5. Проблемы эмпирического базиса. – В кн. «Логика и рост
научного знания». М., Прогресс, 1983. С.124-148.
4.
Мендель Г. Опыты над растительными
гибридами.// Труды бюро по прикладной ботанике. 1910. Т.3. №11. С.479-529.
(Отдельное издание: М.-Л., 1935).
5.
Колмогоров А.Н. Об одном новом
подтверждении законов Менделя.// Доклады АН СССР. 1940.Т.27. С.38-42.
6. Тутубалин В.Н., Барабашева Ю.М., Девяткова
Г.Н., Угер Е.Г. Критерий Колмогорова и экспериментальная проверка законов
наследственности Менделя.
//http://ecology.genebee.msu.ru/3_SOTR/CV_Barabasheva_publ/Kolm-Mend-2008.pdf
7.
Ермолаева Н.И. Еще раз о «гороховых
законах».//Яровизация, 1939. №6
8.
Енин Т.К. Менделизм в селекции гороха.//Докл. ВАСХНИЛ,1939,
№5-6, с.11-16.
9. Darbishire
A.D. An Experimental Estimation of the Theory of Ancestral Contributions in Heredity.// Proc. Royal Soc. Lond. Ser. B. 1909.
No 81(545), pp.61-79.
10. Тутубалин В.Н., Барабашева Ю.М., Девяткова Г.Н., Угер Е.Г. Анализ работ Гаузе по динамике численностей видов.// http://ecology.genebee.msu.ru/3_SOTR/CV_Barabasheva_publ/Analiz-rabot-Gause.pdf
11. Гаузе Г.Ф. Экспериментальное исследование борьбы за существование между Paramaecium Caudatum, Paramaecium Aurelia и Stylonychia Mytilus.// Зоологический журнал. 1934. Том XIII, вып 1, стр 1-17.
12.
Тутубалин В.Н., Барабашева Ю.М.,
Девяткова Г.Н., Угер Е.Г. Идеи В.В. Налимова в математическом образовании
биологов.// http://nalimov.genebee.msu.ru